DKL logo
Our log / Article

Basic operations in H3

This article builds on Introduction to H3 and presents basic H3 operations in Python. Although the core library is written in C, there are bindings for many other languages. H3 supports efficient spatial analysis through key functions, such as converting coordinates to indexes, finding neighboring cells, and computing distances.

image of Víctor Centelles
Víctor Centelles
Software Architect
December 4th, 2025

    Lat/Long to H3 index conversion

    This operation converts a specific geographic coordinate (latitude and longitude) into a unique H3 hexagonal index at a specified resolution.

    Function:

    Lat/Long to H3 index conversion 
          
import h3

lat, lng = 37.769377, -122.388903
resolution = 9

h3_idx = h3.latlng_to_cell(lat, lng, resolution)
# h3_idx = h3.geo_to_h3(lat, lng, resolution)  # ► in v3.x

print(h3_idx)

# Output: 89283082e73ffff
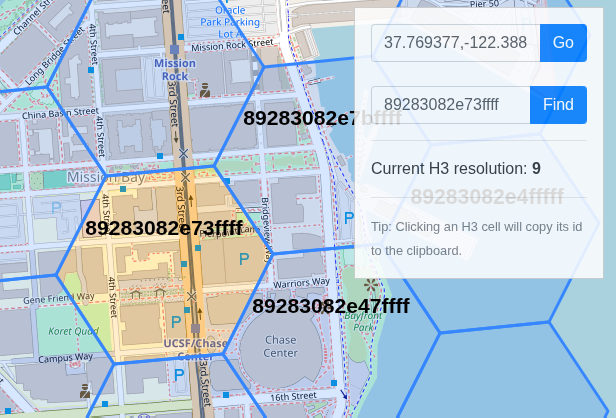
    article image

    Lat/Long to H3 index conversion (image from https://clupasq.github.io/h3-viewer/)

    Full view

    H3 index to Lat/Long conversion

    The reverse operation converts an H3 index back into the geographic coordinates of the hexagon's center.

    Function:

    snippet.python 
          
import h3

h3_idx = '89283082803ffff'

coordinates = h3.cell_to_latlng(h3_idx)
# coordinates = h3.h3_to_geo(h3_idx)  # ► in v3.x

print(coordinates)

# Output: (37.773515097238146, -122.4182710369247)
    Full view

    Finding neighboring hexagons

    You can identify the cells immediately surrounding a specific index using the k_ring function. This is essential for analyzing proximity and spatial smoothing,.

    Function (where k is the ring size; k=1 returns immediate neighbors):

    Finding neighboring hexagons 
          
import h3

h3_idx = '873975442ffffff'

neighbors = h3.grid_disk(h3_idx, k=1)
# neighbors = h3.k_ring(h3_idx, k=1)   # ► in v3.x

print(neighbors)

# Output
# ['873975442ffffff', 
# '873975455ffffff', 
# '873975451ffffff', 
# '87397545cffffff', 
# '873975443ffffff', 
# '873975440ffffff', 
# '873975446ffffff']
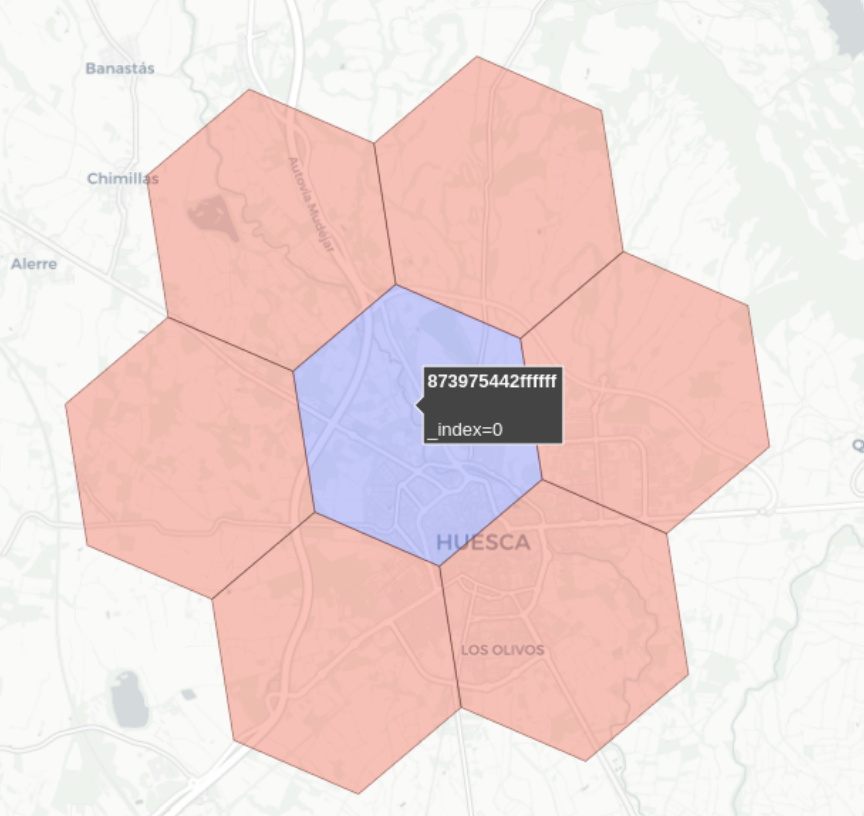
    article image

    Neighboring hexagons

    Full view

    Determining hexagon hierarchy (parent/children)

    H3 is hierarchical, allowing you to move between resolution levels. You can find the smaller subdivisions ("children") of a hexagon or the larger container ("parent") hexagon.

    Functions:

    Returns the finer hexagons contained within the index.

    Returns the coarser parent index.

    Determining hexagon hierarchy (parent/children) 
          
import h3

h3_idx = '873975442ffffff'

children = h3.cell_to_children(h3_idx)
# neighbors = h3.k_ring(h3_idx, k=1)   # ► in v3.x

print(children)
# Output:
# ['8839754421fffff',
# '8839754423fffff',
# '8839754425fffff',
# '8839754427fffff',
# '8839754429fffff',
# '883975442bfffff',
# '883975442dfffff']

parent = h3.cell_to_parent('8839754421fffff')
# parent = h3.h3_to_parent('8839754421fffff')  # ► in v3.x

print(parent)
# Output: '873975442ffffff'
    Full view

    Obtaining the H3 cell area

    This operation calculates the physical area of a specific H3 cell, which defaults to square kilometers (km²).

    Function:

    Obtaining the H3 cell area 
          
import h3

h3_idx = '873975442ffffff'

area = h3.cell_area(h3_idx)

print(area)
# Output: 5.036490172849032

h3.cell_area(h3_idx, 'm^2')
# Output: 5036490.172849031
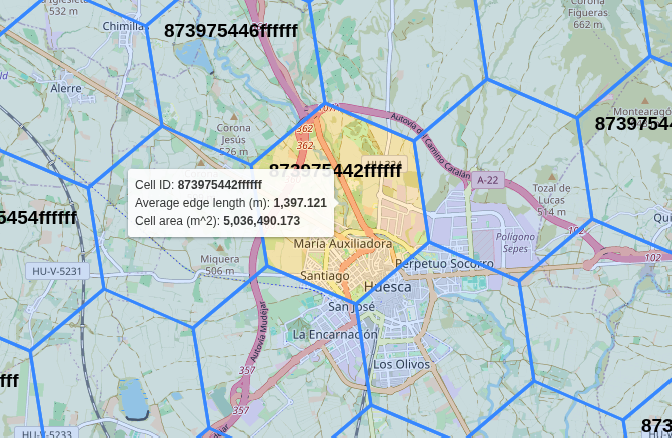
    article image

    Obtaining H3 cell area (image from https://clupasq.github.io/h3-viewer/)

    Full view

    Distance between H3 cells

    H3 allows you to calculate the grid distance between two cells. This is the number of steps required to move from one hexagon to another on the grid.

    Function:

    Distance between H3 cells 
          
import h3

# Neighboring cells 

c1 = '873975473ffffff'
c2 = '873975454ffffff'
c3 = '873975450ffffff'

print(h3.grid_distance(c1, c2)) # Output: 1
print(h3.grid_distance(c2, c3)) # Output: 1
print(h3.grid_distance(c1, c3)) # Output: 2

# print(h3.h3_distance(c1, c2)) # Output: 1   # ► in v3.x
# print(h3.h3_distance(c2, c3)) # Output: 1   # ► in v3.x
# print(h3.h3_distance(c1, c3)) # Output: 2   # ► in v3.x
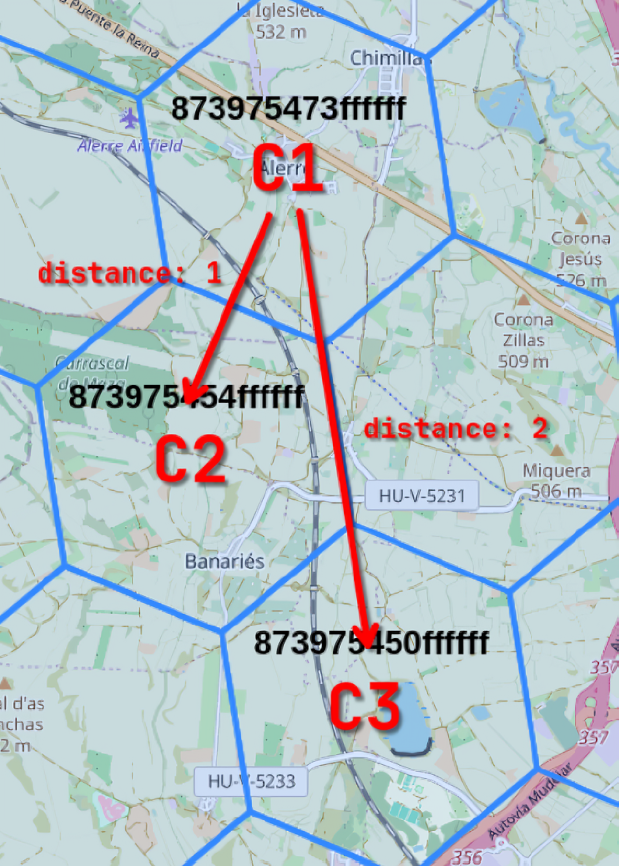
    article image

    Distance between H3 cells (image from https://clupasq.github.io/h3-viewer/)

    Full view