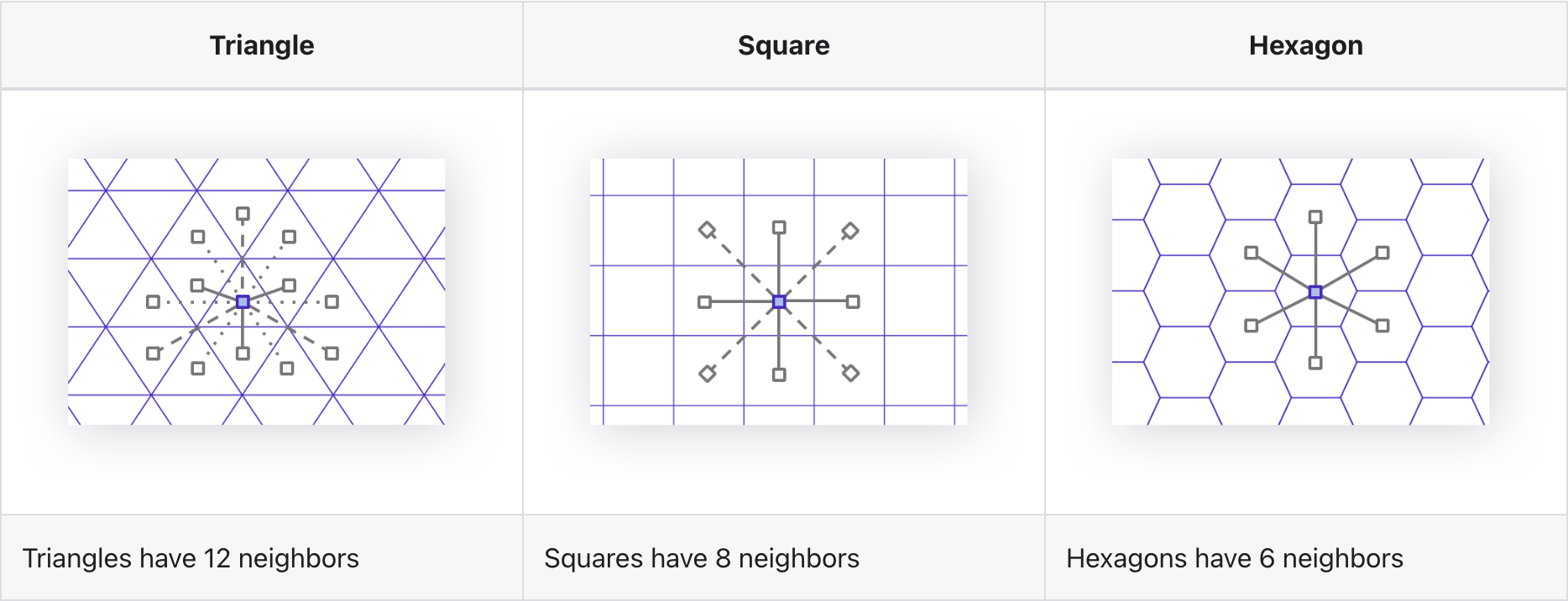
Hexagons have better neighbors
We are all intuitively familiar with square grids. They are the foundation of pixels on our screens and the grid lines on city maps. When we think of dividing up a space, squares are often the first shape that comes to mind.
However, for analyzing movement and proximity, squares have a significant flaw. A square cell has eight neighbors, but they aren't all created equal. The four neighbors at the cardinal directions (north, south, east, west) are closer to the center than the four neighbors on the diagonals. This difference in distance complicates algorithms that need to find the "nearest" of anything.
In contrast, a hexagon's geometry provides a key advantage: all six of its neighbors are equidistant from its center. This uniformity is a brilliant solution that dramatically simplifies spatial analysis. This geometric purity enables a range of algorithms and optimizations based on the grid, including nearest neighbors, shortest path, and gradient smoothing, making it vastly more efficient to find the closest driver or model how a phenomenon spreads across an area.